Для вычисления значения интеграла, хотя и приближенного, существует прекрасный метод, названный в честь его создателя, – метод Симпсона. Он также называется способом парабол, потому как в нем используется построение параболы. Данная фигура строится максимально приближенно к функции. Собственно, так как построить параболу, у которой точки точно совпадают с точками функции, невозможно, интеграл и находится приближенно. Формула нахождения его с границами a и b выглядит вот так: 1/h*(y0+4y1+2y2+4y3+…+4yn-1+yn). Здесь нам нужно просто вычислять каждый y от 0 до n, где n мы определяем сами – чем больше, чем лучше, ведь чем больше будет y-ов, тем более приближенное к истинному у нас значение получится. Что касается h, то это шаг и рассчитывается по такой формуле: (b-a)/(n-1).
 Вам будет интересно:Аккумуляторы ААА и способы их зарядки
Вам будет интересно:Аккумуляторы ААА и способы их зарядки
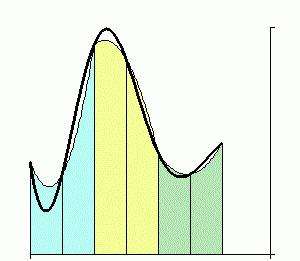
В теории все довольно просто, но нужно было бы реализовать все это на практике. Для многих программистов нет лучшего способа для решения такой задачи, как метод Симпсона – Паскаль или Делфи. В данной среде можно очень просто не только вычислить интеграл, а и построить к нему график функции и даже выстроенную к ней трапецию. Итак, разберемся, как можно быстро реализовать метод Симпсона и при желании даже самим объяснить, как здесь и что организовано, всем интересующимся.
Но перед этим вспомним, как выглядит интеграл. Это фигура, которая ограничена линиями, начинающимися на оси иксов, то есть а и b.

Итак, для начала в программе нужно создать функцию для интегрируемой функции (простите за тавтологию), в которой просто нужно написать f:= и то, для чего будем находить интеграл. Здесь крайне важно не ошибиться в вводе функции на языке Паскаль. Но это отдельная тема для разговора. Полученный код будет выглядеть примерно так:
function f(x:real):real;
И основной текст функции
begin
f:=25*ln(x)+sin(10); {вот здесь и нужно написать содержимое своей функции}
end;
Дальше напишем функцию для реализации метода Симпсона. Начало будет примерно такое:
function simpsonmetod(a,b:real;n:integer):real;
Далее объявим переменные:
var
s:real; { Промежуточные суммы (дальше поймете) }
h:real; { Шаг }
my:integer; { Просто счетчик }
mno:integer; { Очередные множители }
А теперь, собственно, сама программа:
begin
h:=(b-a)/(n-1); { Рассчитываем шаг по стандартной формуле. Иногда в задании пишется шаг, в таком случае эта формула не применяется }
s:= f(b)+ f(a); { Задается начальное значение шага }
mno:=4; { Вспомните формулу - 1/h*(y0+4y1… вот эта 4 здесь и пишется, второй множитель будет 2, но об этом дальше }
Теперь та самая основная формула:
for my:=1 to n-2 do begin
s:=s+mno*f(a+h*му); { К сумме добавляем очередной множитель, умноженный на 4*yn или 2* yn }
if (mno=4) then mno:=2 else mno:=4;{ Тут и меняется множитель - если сейчас равен 4, то меняется на 2 и наоборот}
end;
simpsonmetod:=s*h/3; { Далее полученную в результате цикла сумму множим на h/3 согласно формуле}
end.
Вот и все – делаем все действия согласно формуле. Если вы еще не поняли, как применить в основной программе метод Симпсона, пример вам в этом поможет.
Итак после написания всех функций пишем
Begin
n:=3; { Задаем n }
q:=simpsonmetod(a,b,n); { Так как метод Симпсона заключается в том, чтобы вычислять интеграл от a до b, будет несколько шагов вычисления, поэтому организовываем цикл }
repeat
q2:=q; { Запоминается предыдущий шаг }
n:=n+2;
q:=simpsonmetod(a,b,n); { И рассчитывается следующее значение }
until (abs(q-q2)<0.001);{ В задании пишется точность, поэтому пока не достигнется необходимая точность, нужно повторять те же действия }

Вот такой он – метод Симпсона. На самом деле ничего сложного, пишется все очень быстро! А теперь открывайте свой Турбо Паскаль и начинайте писать программу.
