Довольно часто программисты, даже начинающие, сталкиваются с тем, что есть набор чисел, в котором необходимо найти определенное число. Вот эту коллекцию называют массивом. А чтобы найти нужный элемент в нем, есть огромное множество способов. Но самым простым среди них по праву можно считать бинарный поиск. В чем же заключается данный метод? И как реализовать бинарный поиск? Паскаль является самой простой средой для организации такой программы, поэтому будем использовать именно его для изучения.
Сначала разберем, в чем преимущества этого метода, ведь так мы сможем понять,
 Вам будет интересно:Эвристический анализ в современном мире
Вам будет интересно:Эвристический анализ в современном мире

какой смысл в изучении данной темы. Итак, предположим, есть массив с размерностью хотя бы 100000000 элементов, в котором нужно найти определенный. Конечно, эту задачу легко можно решить простым линейным поиском, при котором мы с помощью цикла будем сравнивать искомый элемент со всеми теми, что есть в массиве. Проблема в том, что реализация этой идеи будет занимать слишком много времени. В простой паскалевской программе на несколько процедур и с тремя строчками основного текста вы этого не заметите, но когда приступите к более-менее крупным проектам с большим количеством разветвлений и неплохим функционалом, готовая программа будет грузиться слишком долго. Особенно в том случае, если у компьютера будет слабая работоспособность. Поэтому и существует бинарный поиск, который сокращает время поиска как минимум вдвое.
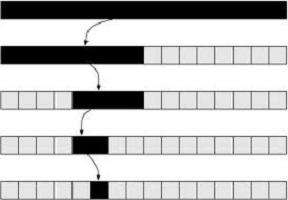
Итак, в чем же заключается принцип работы данного метода? Сразу стоит сказать, что работает бинарный поиск не в любом массиве, а только в отсортированном наборе чисел. На каждом следующем шаге берется средний элемент массива (имеется в виду по номеру элемента). Если искомое число больше среднего, значит все то, что находится слева, то есть меньше среднего элемента, можно отбросить и не искать там. И наоборот, если меньше среднего – среди тех чисел, что справа, можно не искать. Дальше выберем новую область поиска, где первым элементом станет средний элемент всего массива, а последний так и останется последним. Средним же числом новой области станет ¼ всего отрезка, то есть (последний элемент + средний элемент всего массива)/2. Опять производится та же операция – сравнение со средним числом массива. Если искомая величина меньше среднего, отбрасываем правую часть, и так же делаем дальше, пока вот этот средний элемент не окажется искомым.
Конечно, лучше всего посмотреть на примере, как пишется бинарный поиск. Pascal здесь подойдет любой - версия не важна. Напишем простую программу.
В ней будет массив от 1 до h под названием "massiv", переменная, обозначающая нижнюю границу поиска, названная "niz", верхняя граница, названная "verh", средний элемент поиска - "sredn"; и искомое число - "isk".
Итак, сначала назначаем верхнюю и нижнюю границы интервала поиска:
niz:= 1; verh:= h + 1;
Затем организовываем цикл "пока нижняя меньше верхней границы":
While niz < verh - 1 do begin
На каждом шаге делим отрезок на 2:
sredn:= (niz + verh) div 2; {используем функцию div, потому что делим без остатка}
Каждый раз проводим проверку. Если средний равен искомому, прерываем цикл, так как нужный элемент уже найден:
іf sredn=isk then break;
Если средний элемент массива больше искомого, отбрасываем правую часть, то есть верхней границей назначаем средний элемент:
if massiv [sredn] > isk then verh:= sredn;
А если наоборот, то его делаем нижней границей:
else niz := sredn; end;
Вот и все, что будет в программе.
Разберем, как будет выглядеть бинарный метод на практике. Возьмем такой массив: 1, 3, 5, 7, 10, 12, 18 и будем искать в нем число 12.
Всего у нас 7 элементов, поэтому средним будем четвертый, его значение 7.
| 1 | 3 | 5 | 7 | 10 | 12 | 18 |
Так как 12 больше 7, элементы 1,3 и 5 мы можем отбросить. Дальше у нас осталось 4 числа, 4/2 без остатка равно 2. Значит, новым средним элементом будет 10.
| 7 | 10 | 12 | 18 |
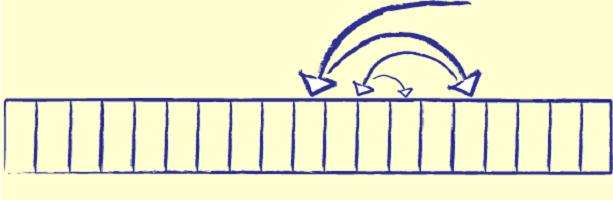
Так как 12 больше 10, отбрасываем 7. Остается только 10, 12 и 18.
Здесь средний элемент уже 12, это и есть искомое число. Задача выполнена – число 12 найдено.
